Skip to contents

Ratio-based position scales for continuous data (x & y)

scale_ratio.Rd

scale_x_ratio and scale_y_ratio are alternatives to traditional scale_*_continuous scales for continuous x and y aesthetics, to explicitly highlight multiplicative or geometric value changes. Rather than traditional log transformations (as in scale_*_log10()), which rescale the axis and return tickmarks on the original scale of the data, scale_*_ratio axis tick values represent a multiplicative change from a reference point. These scales may be especially useful for highlighting proportional changes.

Usage

scale_y_ratio(tickVal = "divMult", ...)

scale_x_ratio(tickVal = "divMult", ...)

Arguments

tickVal

Character, one of "divMult", "propDiff", "percDiff", "nel", or "centiNel"

...

Additional arguments passed to scale_y_continuous or other scale elements (e.g., breaks, labels, etc. )

Details

Logarithmic transformations make multiplicative changes additive, and are often used to highlight relative change. It is traditional to rescale an axis logarithmically and mark ticks with original scale values (e.g. scale_y_log10)). scale_*_ratio provides an alternative, marking ticks with transformed values. This may be especially useful when comparing relative changes of quantities with different units.

Five ratio scales are provided (and denoted with the tickVal argument):

  • divMult rescales an axis logarithmically, and prints multiplicative changes for axis ticks, explicitly noting the operator ( \(\times\) or \(\div\)). This scale highlights symmetry between division and multiplication (\(a \times 2\) is equally far from \(a\) as is \(a \div 2\)).

  • nel rescales an axis logarithmically, and marks it in units of "nels" (for _N_atural _L_ogarithm).

  • centiNel rescales an axis logarithmically, and marks it in units of "centinels," i.e. one hundredth of a "nel". These may be more appropriate for small changes (i.e. of a few to a few hundred percents)

-propDiff rescales an axis logarithmically, but marks axes in terms of a proportional difference from the reference point. Unlike when proportions are plotted on an arithmetic scale, the propDiff transformation reveals underlying geometric symmetry: (\(a \times 2\) is equally far from \(a\) as is \(a \div 2\)) graphically, but tick values indicate the more familiar proportional changes \(+ 1\), \(-0.5\).

-percDiff rescales an axis logarithmically, but marks axes in terms of a percentage difference from the reference point. Unlike when percentages are plotted on an arithmetic scale, the percDiff transformation reveals underlying geometric symmetry: (\(a \times 1.25\) is equally far from \(a\) as is \(a \div 1.25\)) graphically, but tick values indicate the more familiar proportional changes \(+ 25\%\), \(- 20\%\).

For small changes, "centinels" and percentage difference may be preferable, while for larger changes, "nels" (and possibly proportional difference) may be preferable.

Typically, the data passed to scale_*_ratio should be centered on a reference value in advance.

Examples


smaller <- data.frame(x = 1:10, y = exp(seq(-0.2, 0.7, 0.1)))
bigger <- data.frame(x = 1:10, y = exp(-2:7))
ax2 <- ggplot2::sec_axis(
          labels = function(x) {x}
          , transform = ~.
          , breaks = breaks_divMult(n = 7, splits = 2)
          , name = "original scale"
        )

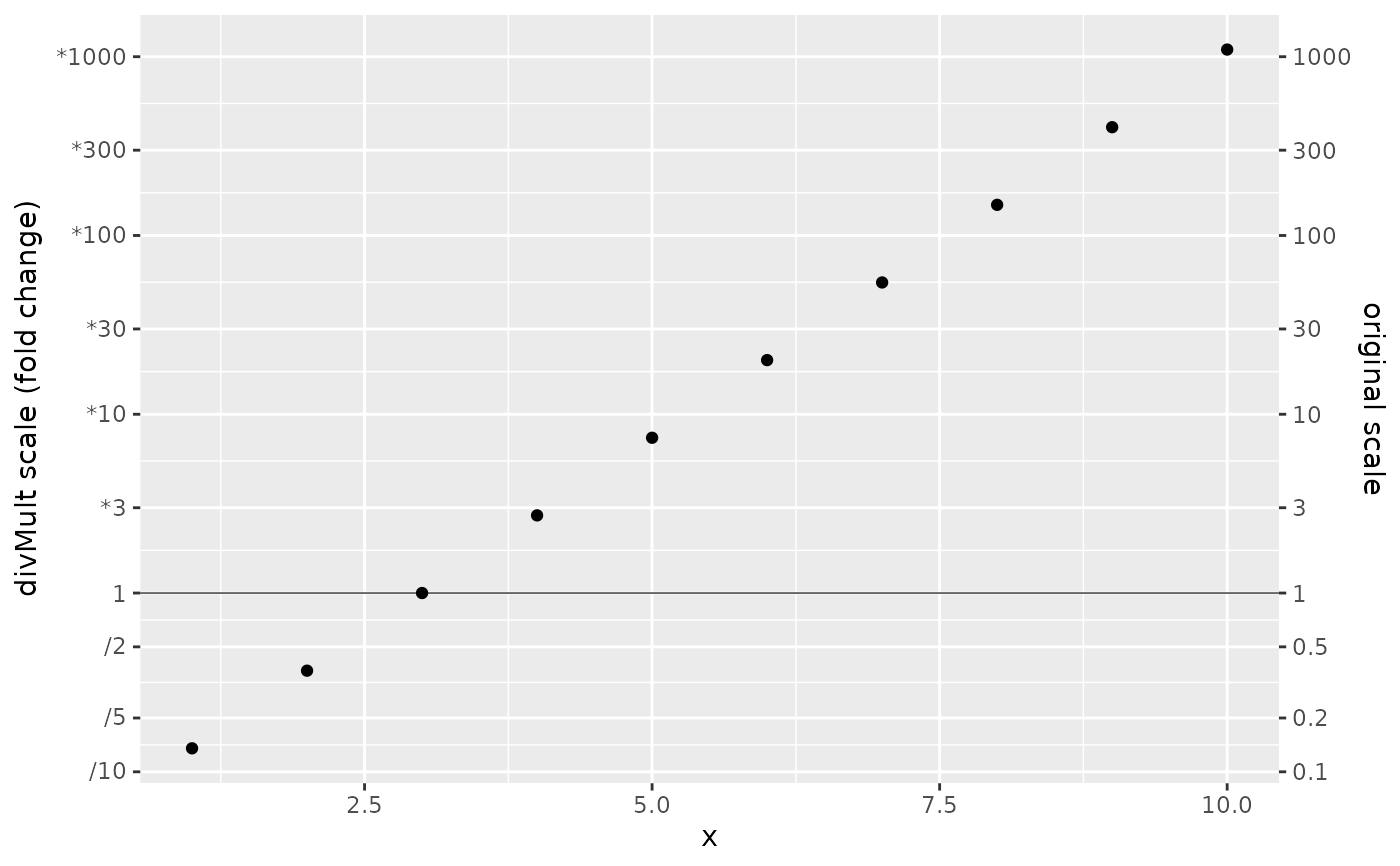
bigger %>%  ggplot2::ggplot(ggplot2::aes(x,y)) +
     ggplot2::geom_point() +
     ggplot2::geom_hline(yintercept = 1, linewidth = 0.2) +
     scale_y_ratio(tickVal = "divMult"
     , slashStar = TRUE
     , sec.axis = ax2
     ) +
        ggplot2::labs(y = "divMult scale (fold change)")


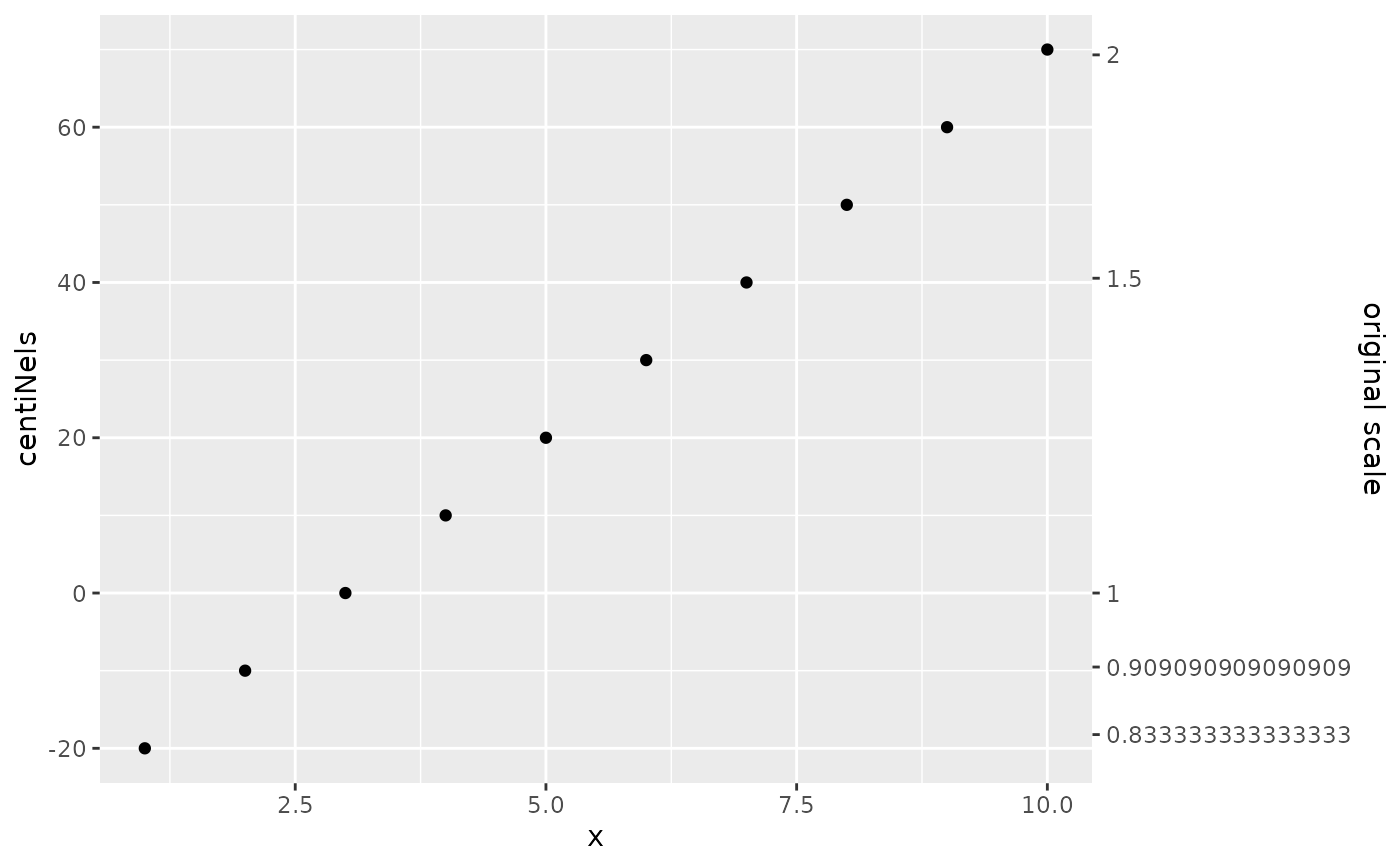
smaller %>%  ggplot2::ggplot(ggplot2::aes(x,y)) +
     ggplot2::geom_point() +
     scale_y_ratio(tickVal = "centiNel"
    , sec.axis = ax2
     ) +
        ggplot2::labs(y = "centiNels")


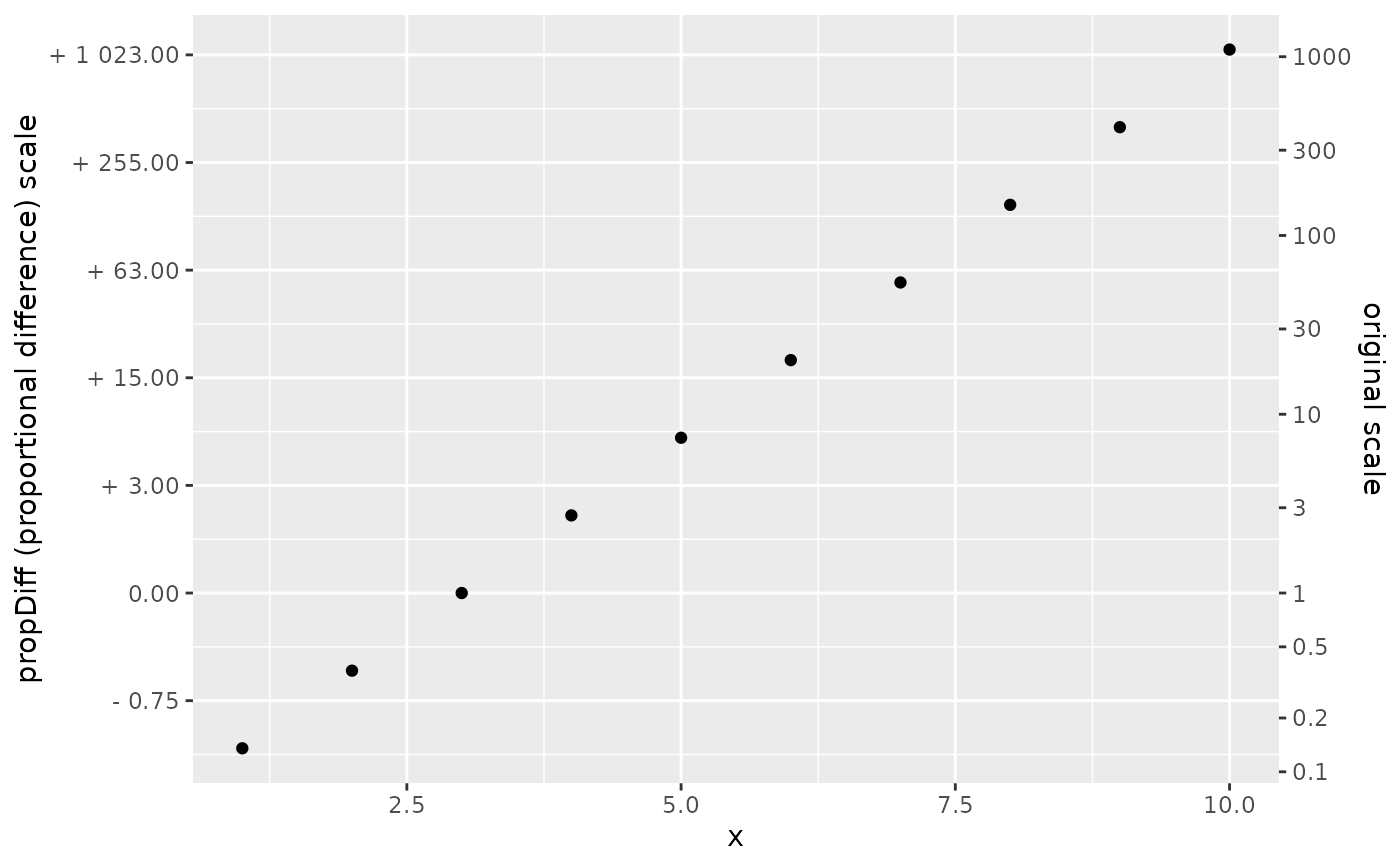
# propDiff is a little strange
bigger %>%  ggplot2::ggplot(ggplot2::aes(x,y)) +
     ggplot2::geom_point() +
     scale_y_ratio(tickVal = "propDiff"
                   , sec.axis = ax2
        ) +
        ggplot2::labs(y = "propDiff (proportional difference) scale")
#> Warning: 'base = 2' chosen by defaut. Setting base of log affects breaking function behavior, and 'exp(1)' may give strange-looking numbers for the propDiff scale


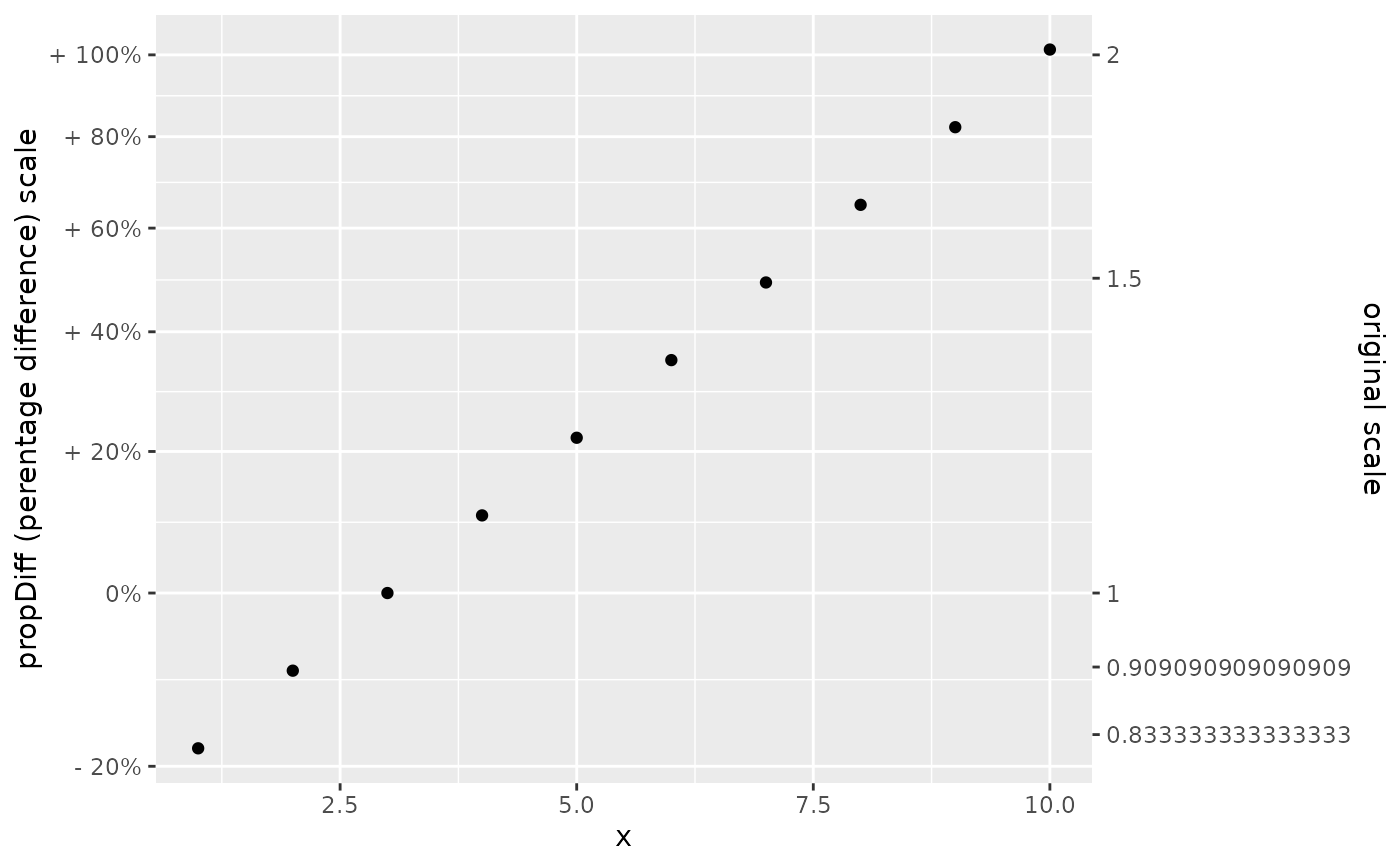
# percDiff should be familiar
smaller %>%  ggplot2::ggplot(ggplot2::aes(x,y)) +
     ggplot2::geom_point() +
     scale_y_ratio(tickVal = "percDiff"
     , sec.axis = ax2) +
        ggplot2::labs(y = "propDiff (perentage difference) scale")